初识 部分求值 与 二村映射

Maybe Amadeus

21 👍 / 0 💬

Glomzzz (Glomzzz) (github.com)

话说已经三周没有提交代码了呢，其实这段时间我在憋大招：

- 一个完成了第一二三类二村映射的部分求值语言 (其实应该叫 mix)

简短讲一下什么是二村映射

部分求值

mix 是一个部分求值程序，以第一个参数（一般是一段程序）为基础，它能够用第二个参数对其进行特化(specialize)，得到特化后的新的程序，并且它能够不断地特化剩余程序

剩余程序：已经特化过的程序

{\normalsize \begin{align*} mix(f,arg) &= specialize\,\,\,f\,\,\,with\,\,\,arg \\ \end{align*} }


arg的格式，我们用(name,value) 来表示，name指f的参数名之一，value指参数值 例如，这样一段程序：

def search(nameList,valueList,name):
  while head(nameList) != name:
      nameList = tail(nameList) 
      valueList = tail(valueList) 
  return head(valueList)

当我们用("name","z")与 ("nameList",["x", "y", "z"]) 先后去特化search时：

def search_1(nameList,valueList):
  while head(nameList) != "z":
      nameList = tail(nameList) 
      valueList = tail(valueList) 
  return head(valueList)
def search_2(valueList):
  return head(tail(tail(valueList)))

{\begin{align*} search\_1&=mix(search,(''name'',\,\,''z'')) \\ search\_2&=mix(search_1,(''nameList'',\,\,[''x'',\,\, ''y'',\,\, ''z''])) \end{align*} }

可以看出，search_2 显然会运行得更快，因为它已经在特化时期完成了很大一部分计算。

方便起见，我们：

第一类 二村映射

首先， target_TS 是我们的目标程序(下标T表示 target 是由S语言写的，如果没有下标那就不限定语言)，

显然，我们有以下等式：

{\begin{align*} target_T(data) &= interpreter_L(source_S,\,data) \\ &= result \end{align*} }

L : 实现解释器的语言
S : 源语言
M : 实现mix程序的语言
T : 目标程序语言

不难察觉出，我们可以利用mix去特化 interpreter ，那么：

{\begin{align*} target_T(data) &= interpreter_L(source_S,\,data) \\ &= mix_M(interpreter_L,\,source_S)(data) \\ &= result \end{align*} }

你也许会对 M，S，L，T 这几个语言之间的关系产生疑惑——Don't worry！
我会慢慢讲解的！

让我们讨论一下 M，S，L，T 这四个语言之间的关系：
为了保证 mix_M 能够不断地特化剩余程序，当然要能继续特化 target_T ，
我们的语言T需要是能够mix_M被特化的，也就是说， T\,\,=\,\,L

其实，这就是第一类二村映射：

{\begin{align*} target_L &= mix_M(interpreter_L,source_S) \end{align*} }

附：

\begin{align*} &mix_M \,\,\,\,&&:\,\,\,\, program_L \to arg \to residual_program_L \\ &interpreter_L \,\,\,\,&&:\,\,\,\, source_S \to data \to result \\ &target_L &&:\,\,\,\, data \to result \end{align*}

注意 target_L = mix_M(interpreter_L,source_S) 的类型是如何推导出来的。

符合直觉的类型推导：
若 g_L \,\,:\,\, A \to B \to C
则 mix_M(g_L,a:A)\,\,:\,\,B \to C

第二类 二村映射

延续第一类二村映射的结论，下列等式显然成立，

{\begin{align*} target_L &= mix_M(interpreter_L,source_S) \\ &= compiler_C(source_S) \end{align*} }

通过观察，我们可以发现：如果用 interpreter_L 对 mix_M 进行特化，那么就会得到与 compiler_C 效果相同的东西，也就是一个 compiler_{C_2}

所以：

{\begin{align*} compiler_{C_2} &= mix_M(mix_M,interpreter_L) \end{align*} }

好，让我们推导一下 {C_2} ，M，L 之间的关系： 首先由第一类二村映射中的推导可知： mix_M 能够特化 L 的程序 并且，mix_M可以生成出它仍能够继续特化的剩余程序 compiler_{C_2}

所以： C_2\,\,=\,\,M \,\, = \,\, L

即： {\begin{align*} compiler_L &= mix_L(mix_L,interpreter_L) \end{align*} }

附： \begin{align*} &mix_L \,\,\,\,&&:\,\,\,\, program_L \to arg \to residual\_program_L \\ &interpreter_L \,\,\,\,&&:\,\,\,\, source_S \to data \to result \\ &compiler_L &&:\,\,\,\, source_S \to data \to result \end{align*}

注意 compiler_L = mix_L(mix_L,interpreter_L) 的类型是如何推导出来的。

这是大概特化的过程：

arg 取第一个参数（直观起见）， residual\_program_L 取剩余的，于是：



这意味着：

如果你想要在语言L中实现语言S的第二类二村映射，你需要用语言 L 本身去写出：

- mix_L(pgm_L,arg_L)

- interpreter_L(source_S,data)

第三类 二村映射

你可以先在这里暂停一下，模仿第一类二村映射与第二类二村映射的推导，去推出第三类二村映射。

让我们开始吧！

延续第二类二村映射的结论，下列等式显然成立，

{\begin{align*} compiler_L &= mix_L(mix_L,interpreter_L) \\ &= cogen_G(interpreter_L) \end{align*} }

cogen 是 compiler_generator 的简写！

通过观察，我们可以发现：如果用 mix_L 对 mix_L 进行特化，那么就会得到与 cogen_G 效果相同的东西，也就是一个 cogen_L (这里的显然是L)

所以：

{\begin{align*} cogen_L &= mix_L(mix_L,mix_L) \end{align*} }


附： \begin{align*} &mix_L \,\,\,\,&&:\,\,\,\, program_L \to arg \to residual\_program_L \\ &cogen_L &&:\,\,\,\, program_L \to arg \to residual\_program_L \end{align*}

大致特化过程：

arg 取第一个参数（直观起见）， residual\_program_L 取剩余的，于是：

可以看出 cogen_L 不仅仅是一个 compiler generator，它也可以用作其它用途（）

这实在是太不直观了！

之后通过具体实现我们可以更确切地感受到 cogen ，所以期待一下后面的文章吧！


如果你想要在语言L中实现语言S的第三类二村映射，你需要用语言 L 本身去写出：

- mix_L(pgm_L,arg_L)

所以第二类二村映射的实现已经够用来实现第三类二村映射了！

More。。。

你可以试着顺着这个思路继续往下推导出第N类

你会发现后面是无穷无尽的 mix(mix,mix)

看到这里，你可能想问：这么"套娃"有什么意义呢？

众所周知，软件工程没有银弹，但是后端可以塞跳弹（bushi

那么部分求值，以及这几个二村映射的缺点是什么呢？

如果没有具体实现的代码，这很难直观地体验出来，

事实上，部分求值会在特化时导致代码膨胀，具体的细节让我们日后再说。

附上Benchmark：

The run times are measured in Sun 3/50 cpu seconds using Chez Scheme, and include garbage collection.


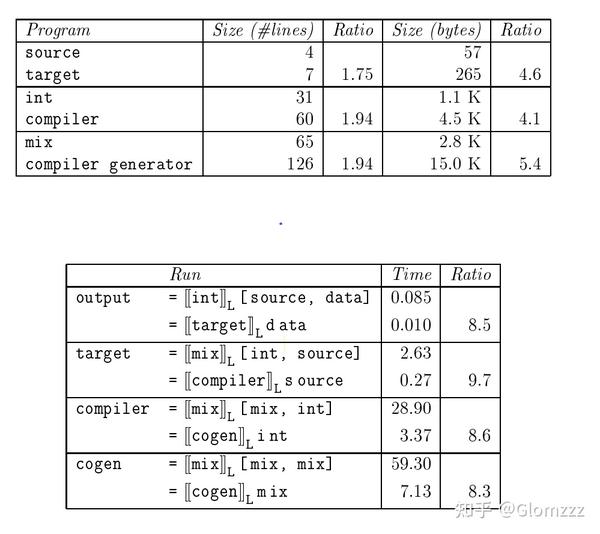
下一篇：第一个部分求值程序mix！

引用

Partial Evaluation Book

鸣谢

（按首字母排序

专栏：Glomzzz的文章