【强化学习与最优控制】笔记（三）动态规划求解实际问题举例

上一期笔记，忘记的小伙伴可以复习一下：

王源：【强化学习与最优控制】笔记（二）随机性问题的动态规划

没有教材的同学可以从如下链接中关注公众号并且在公众号后台回复“强化学习2021”即可获取电子版教材的草稿版本：

Dimitri P. Bertsekas 强化学习2021版教材和视频课程推荐

前两期的回顾，没有看或者忘记的童鞋可以复习一下：

王源：【强化学习与最优控制】笔记（一）确定性问题的动态规划

王源：【强化学习与最优控制】笔记（二）随机性问题的动态规划

1 最短路问题

在开始最短路问题之前让我们回顾一下动态规划的核心公式：

最短路问题定义：在一个图中求2个节点之间最短的路径。

最短路问题一般需要假设图中所有的圈的路径非负。因为如果有负的圈的话一直在这个圈子里绕就可以让路径趋于无穷小。

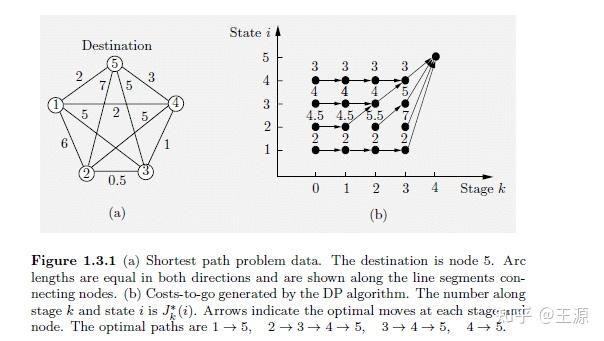
如上图中(a) 所示是给出的无向图，节点5是我们的终点，节点1,2,3,4是起点。在这个最短路问题中比较关键的问题是如何定义stage？

定义为从节点 出发经过个节点到终点 的最优路径长度，其中为总节点数，

由此可得DP的递推公式

这里需要注意的是因为最短路径所经过的节点数我们事先并不知道，如果拿经过节点数目作为 stage的数目的话是比较困难的。因此我们在式(1,3) 的 集合中除了要包含和节点 相连的所有节点 之外，也要包含节点 ，也就是说我们可以停在原地不动。 这样就可以表示出经过节点数小于的路径。

1.1 代码实现

代码主要分为两部分，其中第一部分是输入图的数据。networkx是一个图论计算的包，用它来做一些图论方面的计算非常方便。我们先通过networkx建立一个无向图，然后添加节点，添加边（包含每条边上的权值），对应下面代码 G.add_weighted_edges_from([(0,1,6),(0,2,5),(0,3,2),(0,4,2),(1,2,0.5),(1,3,5),(1,4,7),(2,3,1),(2,4,5),(3,4,3)])，其中（0,1,6）就表示节点0和节点1直接有边连接，并且其权值为6，以此类推，我们按照教材中如图所示把图的边的权值输入进去。Adjacency Matrix矩阵表示图的领接矩阵，对应代码中就是A矩阵，A矩阵中的元素就是节点到节点的距离，也就是我们公式中的

import networkx as nx import numpy as np 
G = nx.Graph() G.add_nodes_from(range(0,5)) 
G.add_weighted_edges_from([(0,1,6),(0,2,5),(0,3,2),(0,4,2),(1,2,0.5),(1,3,5),(1,4,7),(2,3,1),(2,4,5),(3,4,3)]) 
A = nx.adjacency_matrix(G) A = A.todense() print(A)

第二部分是根据公式(1.3-1.4)计算 需要注意的是我们要计算的是对所有stage和所有状态的，因此 在这里是一个二维数组，其维数为阶段数状态数，对应代码第二行的costToGoValue。代码第三行的t表示终点为节点4。然后就先按照公式(1.4) 把最后一个阶段的costToGoValue直接赋值。之后再用循环的方式，依据式(1.3) 把所有阶段的costToGoValue递推得到。

nStage, nState = nx.number_of_nodes(G), nx.number_of_nodes(G) 
costToGoValue = np.zeros((nStage, nState)) t = 4 
costToGoValue[:,-1] = A[:,t].reshape((5)) 
for k in range(nStage-2,-1,-1): 
    for i in range(nState): 
        costToGoValue[i,k] = min([A[i,j] + costToGoValue[j,k+1] for j in range(nState)]) print(costToGoValue)

其实到这来还不算真正的完结，我们仅仅是算出了 。我们真正最终想要的是最优的Policy: ，这个留作大家的homework思考一下，怎么根据 算出 。提示一下在前两节笔记中都有相关内容，想不起来的童鞋可以复习一下。已经熟悉的童鞋可以再代码实现一下加深理解。

2 组合优化问题

很多组合优化问题都可以采用动态规划的框架来求解，我们这里以经典的TSP问题为例（旅行商问题）。旅行商问题是 给定一系列城市和每对城市之间的距离，求访问每座城市一次并回到起始城市的最短回路。TSP是一个非常经典非常常见的运筹学中的组合优化问题。

如下图所示就是一个TSP问题的解，图中的五角星就代表一个城市，图中整体上形成了一条路径把所有的城市连接在了一起，我们就是找到这样一种连接使得其总路径最短。

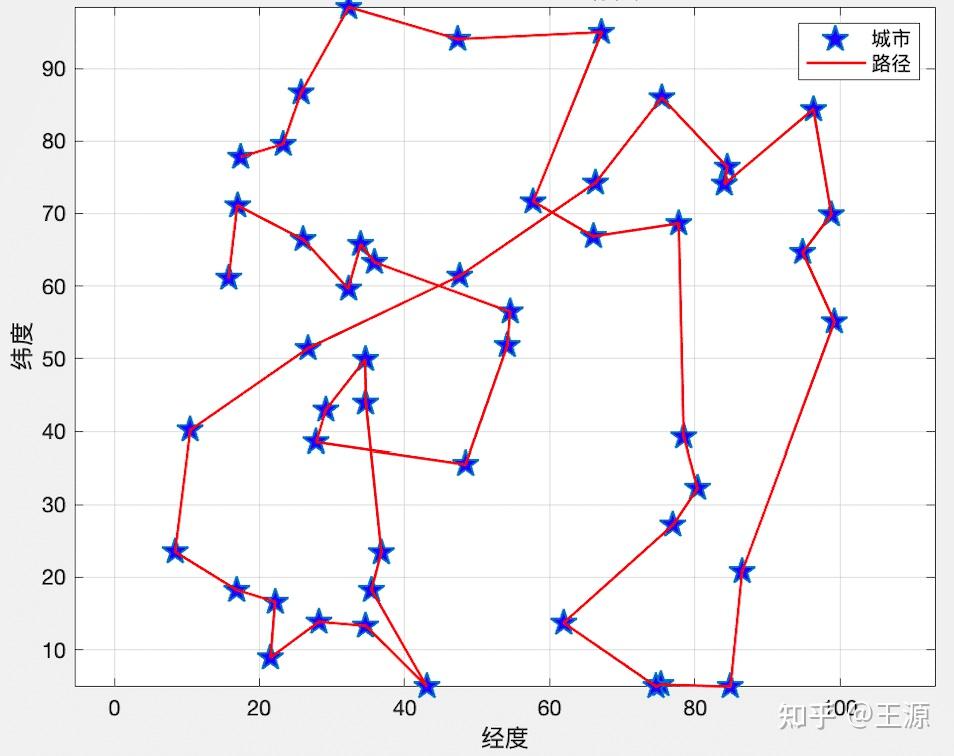
接下来我们就采用动态规划给大家演示一下如何来求解TSP问题，设TSP问题需要经过 个城市，想要采用动态规划求解TSP问题关键就是定义出 state，control 和 system dynamics ，如下所示：

state ： 我们当前所在城市 ，已经访问过的城市的集合

这里需要注意的是状态变量的定义分为两部分，一部分是当前所在城市，另外一部分就是已经访问过的城市的集合（注意这里是集合而不是一个序列，我实际上只需要知道访问过哪些城市而无需知道是以什么顺序访问这些城市的，这一点和原始教材是不一样的，稍后就会看到这么定义状态的好处在于状态变量的维数大大降低）

control： 下一个要去的城市是哪个

system dynamics:

stage cost： 从城市 到城市 的距离

Value function:当前在城市 并且经过集合 中所有城市有且仅有一次的最小距离

完成了上面这些定义之后，接下来就是直接套用动态规划递推公式，设 为出发城市：

看到这里也就是用动态规划解了一下TSP问题了，那么动态规划强大之处在哪里呢？

我们需要对动态规划的计算复杂度进行一些分析，动态规划计算复杂度和两部分有关系一个是stage的数量，一个是状态的数量。stage 的数量易知为 个，状态 由两部分构成，一部分是当前城市最多有 个取法，一部分是集合 实际上是城市集合的一个幂集，每个城市都可以选择在或者不在集合 里，因此集合 大小为 。

那么我们把以上三部分合并起来就得到算法复杂度为 ，也就是说我要最多计算式(2.2) 次就能得到最优解了。那我们又知道如果采用暴力穷举法的话对于TSP问题我们要进行 次计算。

由此得出结论：1 动态规划求解TSP问题的复杂度依然是指数级别，动态规划不可能让；2 动态规划比暴力穷举法的效率要高的多，因为当 比较大的时候 。

到这里我们知道了要想用动态规划完全精确求解组合优化问题 虽然比暴力穷举法计算复杂度低很多，但依然要面临维数灾难的问题。强化学习/近似动态规划就是针对传统动态规划的不足而来的。通过一些近似的方法来降低计算量，解决传统动态规划的问题。

也正是因为采用动态规划直接暴力求解组合优化问题依然是NP-hard的，很多时候我们只需要近似求解即可。尤其是对cost to go function的近似，可以把数学优化里边的各种Programming，各种Relaxation方法，各种Cut的方法，各种启发式算法与动态规划/强化学习结合起来，个人感觉未来将会是组合优化问题有所突破的地方。AlphaGo的成功其实某种程度上已经证明了这一点。对这方面感兴趣的童鞋可以参考这篇文章： Bertsekas D. Rollout algorithms for discrete optimization: A survey[J]. Handbook of Combinatorial Optimization, D. Zu and P. Pardalos, Eds. Springer, 20， 随着后续章节的展开，我们会在后边详细介绍这部分内容，此处就不过多展开介绍了。

3 Linear Quadratic Optimal Control

我们以钢铁生产中的加热炉为例来讲解 Linear Quadratic Optimal Control，如下图所示是钢铁材料在加热炉中的示意图：

从图中可以看到，钢铁材料有一个初始问题，然后经过了2个加热炉（本问题中设定N=2）后会得到最终的温度。由此我们可以定义

: 初始温度 : 第k个炉子的出炉温度 : 第k个炉子所用的燃料量 动态系统：

其中 目标函数有两项，一是让最终出炉的温度 尽量接近给定的目标温度 ，二是让所有炉子消耗的总燃料量最小。由此可得目标函数为 其中 为权值 我们先暂时不考虑其它的约束条件，可以看出目标函数是一个二次项，而动态系统是一个线性系统，所以这个问题被称为 Linear Quadratic Optimal Control(LQR)，请记住这个问题的形式，因为很多的复杂的 控制问题可以转化为 LQR 来近似解决 易知

进一步根据动态规划递推表达式(1.2)可得：

将上式对 求导，令导函数等于0 即可得到最优解的充要条件（因为目标函数是关于 的凸函数）：

由此可得：

将最优的 policy（3.10）反带回到 （3.6）中可得

然后进一步递推到前一个阶段可得：

在上式中带入式(3.12)可得：

进一步利用系统动态的表达式（3.1) 将 替换可得：

同理对 求导后可得最优的 policy，这块和之前对 求导是一样的，这里给出结果：

这个例子告诉我们非常重要的一个结论就是 目标函数是凸二次的（Bertsekas书中原文写的是二次的，没有特别强调凸，我觉得是要加上凸才能满足全局最优的条件），动态系统是线性的，也就是我们所说的 Linear Quadratic Optimal Control，这个问题的性质比较好可以直接得到 的解析形式（closed form）， 在之后的问题中我们基本上都很难获得如此好的一个性质的问题。

强化学习与最优控制（英文版）

下一期笔记：

王源：【强化学习与最优控制】笔记（四）强化学习与最优控制的关联与对比