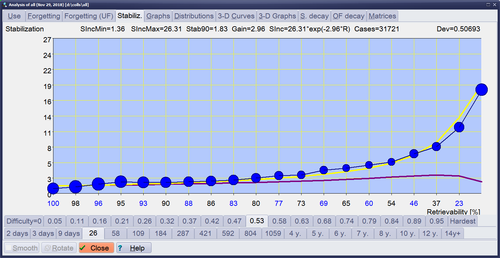
间隔效应是指在较长的时间间隔后成功回忆的 记忆增长幅度更大。
间隔效应可以借助 稳定化曲线来精确表达，该曲线将该效应定义为 记忆稳定化随时间的增长。详见： 稳定化曲线
间隔效应有积极和消极的解释，产生一定程度的困惑：
- 对长间隔的积极解释（又称 稳定化）：如果我们在学习中增加间隔（在一定程度上），就能提高学习效果（即间隔效应是有帮助的）。
- 对短间隔的负面解释：如果我们复习的频率过高，复习的结果会被记忆系统忽略（即间隔效应是有害的）。
在 记忆的双组分模型 [1]中，我们使用了 稳定化函数，它解决了上述困惑，指出每个单独的记忆痕迹都有一个最佳的复习时间，这个复习时间可以使预期的记忆效果最大化，这是 稳定化和遗 忘概率 [2]合成的结果。
由 SuperMemo 中 稳定化曲线的近似值得出的数据表明，增益随着稳定性的提高而明显下降，随着 难度的提高而略有增加。换句话说， Bjork 的老格言是成立的：越难越好。
对于那些不太在意知识长期 保留的人来说， SuperMemo 也可以说是 提高脑力的工具。
也可以看看：
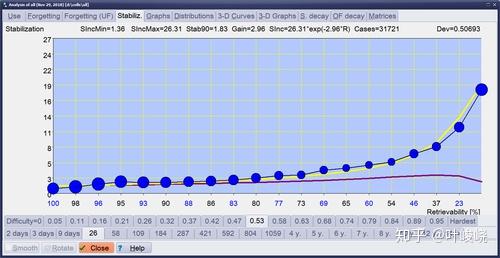
图：用 SuperMemo 计算的 稳定化曲线。水平线显示的是时间，用 记忆可提取性表示。竖线显示 稳定化，即以 记忆稳定性的增长来表示记忆持久性的增加。蓝色圆圈表示在给定的 可提取性水平下， 稳定性随着 复习的进行而增加多少。蓝色圆圈的大小取决于收集到的数据点的数量。该图由进行 31,721次 重复的 SuperMemo 中的数据产生，其中 难度=0.53， 稳定性=26[天]。 稳定性增长从 可提取性=100% 时的 1.36（SIncMin=1.36）增加到 R=0% 时的 26.31（SIncMax=26.31）。SuperMemo 中 R=90% 时的最佳复习产生 1.86 的 稳定性增长(Stab90 相当于旧 SuperMemos 中的 O-Factor)。表示间隔效应的增益常数等于 2.96，即相对较高，因为符合低 稳定性分位数。这个数据集的稳定度可以用公式（黄线）精确计算： ![[公式]](https://picx.zhimg.com/v2-8bb82f6ecabc493ed1cb672dcb224013.jpg?source=7e7ef6e2&needBackground=1)
，产生 0.5069 的微小 偏差。巩固曲线用紫色显示，并表明 遗忘指数是所提出的数据集的一个可信的学习标准。对于 R 接近 100% 时，所呈现的图形的实际 稳定性增长是 0.879，因为是用 2074 次测量得到的。这在图片中并不清晰可见，但可以通过 SuperMemo 中的稳定化矩阵导出进行研究。这意味着稳定化曲线公式在接近 100% 和 0% 的 可提取性的极端情况下可能是不准确的。这可以解释为，没有任何记忆是可以完美提取或可验证地抹去的（见： 我们永远不会忘记）。