总目录:0 目录《间隔重复的历史》
上一章:06 1989: SuperMemo 适应用户记忆(下)
Thoughts Memo 汉化组译制
原文:1990: Universal formula for memory
最优复习与间歇复习
到了 1990 年,我很是笃定我手握着重大发现。我破解了遗忘难题。我知道了记忆简单内容的复习最佳时机。一经在我硕士论文中描述它的许可,我的探索欲也水涨船高。我希望我可以找到一个长期记忆的通用公式,能够让我跟踪记忆在各种形式的检索和接触中的表现形式。
我已经收集了一些数据,这些数据可能会帮助我找到这个公式。在 1985 年发现最佳重复间隔之前,我把问题写在一页页纸上来复习知识。此时复习混乱不堪,由可利用的时间、需要或心情支配。我把这称为「间歇性学习」。我有单个页面和每次复习的回忆数据。虽没有 SuperMemo 的周期性,这种数据也算较为理想。这正是我为解决记忆问题而需要的数据。只不过,这些数据都仅仅记录在纸上。
1990 年春天,我叫我姐姐来打字录入数据。当然,我没有一个妹妹会情愿来做这件事。我的姐姐比我大 17 岁。我利用她对我的爱,让她做这种枯燥繁重的工作,而没有顾及到她的时间。她两年后去世了。我再也没有机会报答她对间隔重复理论的贡献,她甚至没有机会了解这个理论。从 1990 年 5 月 1 日开始,她在我不用电脑的时间,将数据从纸上转移到电脑上。她打字很慢,花了很多天。她的工夫是值得的。
间歇学习模型
在 1990 年的整个夏天,我没有专注于我的硕士论文,而是研究「间歇学习模型」。对我来说,连续工作 10 个小时,感觉没有半点发现而在早上 7 点睡觉,或者让电脑整夜计算数据,都是很正常的。
锲而不舍,捣鼓调整是有代价的。只有少年才能负担得起,他们应该有空间和自由。尽管我已经 28 岁了,家人们还是默默忍受我的一举一动。就像一个不成熟的青少年。我住在我姐姐的公寓里,在那里我可以利用她的善意。在电脑前工作的时间很长,被借口为「在做我的硕士论文」。事实上,没有人要求我这样做,也没有人要求我这样做,它甚至没有推动 SuperMemo 的发展。这是一个纯粹的科学好奇心的案例。我只是想知道记忆是如何工作的。
我有几十页的问题和他们的重复历史。我试图预测「每页的记忆失误」。我使用平方根标准差来预测失误(下面表示为Dev)。到 1990 年 7 月 10 日,星期二,我达到了 Dev<3,感觉问题几乎「解决」了。1990 年 7 月 12 日,我改进到 Dev=2.877(顺便说一下,我的论文中提到了2.887241)。然而,到 1990 年 8 月 27 日,我在那天的笔记中宣布这个问题无法解决。
个人轶事。为什么使用轶事?
1990 年 8 月 27 日:我解决了间歇学习,表明这个问题是无法解决的!单独一个参数无力描述与整页项目的记忆强度。这表明,E 因子较低的项目没有最优间隔!
1990 年 8 月 30 日,我在硕士论文中解说了这个模型。文章一共有 15 页,不算很好读。我打赌没有人有耐心读完整篇文章。90 年代末我的硕士论文节选版发布在网络,而描述间歇学习的这一章甚至没有在 supermemo.com 上发表。
然而,基于该模型得出的结论,深刻地影响了我随后几十年中对记忆的思考。该模型背后的想法,实际上非常类似我在开发 SM-17 算法 (2014-2016) 时应用的优化。
当我宣布这个问题无法解决时,我的意思是我无法准确地描述「困难页」的记忆,因为性质不同的材料需要更复杂的模型。然而,这篇 1990 年 8 月 31 日记录的笔记却对此更加乐观:
个人轶事。为什么使用轶事?
1990 年 8 月 31 日:不间断地研究间歇学习模型。到了晚上,计算机终究没有让我离解决方案更进一步。然而,我有个好主意,就是用 IL 模型的绝世优秀功能计算出最优间隔。屏幕上的结果映入眼帘时,我简直不敢相信我 [哔——] 看到什么。这些正是我在 1985 年发现时试图制定 SuperMemo 方法时发现的间隔。我高兴地在家里跳来跳去,简直像一条有两条尾巴的狗。所以我可以说我真的解决了 IL 问题(对比 1990 年 8 月 27 日)。但我发现,这个成功并不是今天给我发现的一切:
- 最优系数随着连续的间隔而减少(我以前凭直觉感觉是这样的),
- 对于遗忘指数等于 10%,保留率为 94%(如 EVF 数据库)
- 保留率与遗忘指数呈线性关系 [2018 年评论:在异质材料的小范围内](这无法从我 1 月份进行的模拟实验中计算出来)
- 该模型说,遗忘指数的理想值是 5-10%(工作量-保留率的权衡)
- 如果间隔时间是最优时间的两倍,则记忆强度增加最多!!
- 如果遗忘指数为 20%,则记忆强度增加最多
[...] 我的公式只有在间隔比以前的强度短不了多少时才有效。
过去(1990)与现在(2018)的对比
本章末尾的结论,以及程序本身都让人想起我在 2005 年寻找记忆稳定性提高的通用公式时使用的方法,以及在 2014 年,算法 SM-17 是基于对记忆的更精确的数学描述。像最新的 SuperMemo 算法一样,该模型使得计算任何重复计划的保留率成为可能。当然,它的准确度要低得多,因为它基于劣质的数据。此外, SuperMemo 17 所做的实时工作,在 1990 年时需要花费许多小时的 PC 电脑时间。
我的硕士论文中这个看似无聊的老的部分到现在已经变得很重要了。我敢说,只有劣质的数据将这项工作与 25 年后出现的算法 SM-17 相隔甚远。我引用的这段文字在符号和文体上做了些许改进,但没有关于遗忘曲线的章节,该章节由于计算中使用的材料太不同而出现错误。
存档警告:为什么使用文字档案?
这段文字是《优化学习》 作者:Piotr Wozniak (1990) 的一部分
间歇学习模型
SuperMemo 模型为计算最优间隔提供了基础,在时间最优的学习过程中,应该把重复的内容分开。
然而,如果重复的时间间隔不规律,则无法预测记忆变量的变化。
下面我提出一个尝试,以增强 SuperMemo 模型,使其可以用于描述间歇学习的过程。
在第三章中,我提到了,在算法 SM-0 开发之前,我学习英语和生物的方式。
那段时间(1982-1984年)收集的数据为构建间歇学习模型提供了一个很好的基础。遵照最小信息原则制定的项目(通常有成对的词的形式)被分组在页面中,进行不定期的复习过程。
所收集的数据以计算机可读形式提供,包括71页的重复描述,此外,80个类似的页面参与了由SM-0时间表监督的过程。
与算法 SM-17 的相似性
请注意,这个问题的表述让人想起了算法SM-17 中用来计算稳定性增长矩阵(SInc[])的程序。记忆稳定性被重新缩放,以便能够将其解释为一个间隔。甚至符号也是相似的:S 代表稳定性,D 代表偏差。页面遗忘数量代替了可提取性。
我以前喜欢玩各种优化算法。你仍然可以在 SuperMemo 17 中查看该算法做表面拟合优化的可视化(见图片)。12 个变量做处理可能有点低效,但我从不关心处理方法本身如何,只关心能否结果是否可以拓展我对记忆原理的认知。
对于那些熟悉算法 SM-17 的人,我们在下面的文本中改变了符号。此外,我们改变了 In 和 Ln 等符号,这些符号在打印时很容易被误读为对数。
变化清单:
- Ln ->
- In ->
- Dn ->
- R -> RepNo
间歇学习问题的表述
存档警告:为什么使用文字档案?
这段文字是《优化学习》作者:Piotr Wozniak (1990) 的一部分
11.1.间歇学习问题的提出
1. 共有 161 个页面。
2. 每页包含约 40 个项目。
3. 对于每一页,学习过程的描述(在实验重复期间收集)有以下形式:
((-, ),(
,
),(
,
), ...,(
,
))
其中:
- 第 i 次重复前使用的间隔(范围在 1 到 800 之间),
- 在第 i 次重复过程中,遗忘的次数(范围从 0 到 40),
- n - 总重复次数(范围从 3 到 20)。
4. 找到公式所描述的函数 f 和 g:
S(1)=S1
S(n)=f(S(n-1), ,
)
Laps(n)=g(S(n-1), )
其中:
- S(n) - 与第 n 次重复后的记忆强度相对应的任何变量(比较第 10 章),
- 第 n 次重复前使用的间隔;取自间歇学习期间收集的数据,
- 在第 n 次重复中的遗忘数量;取自间歇学习期间收集的数据,
- Laps(n) - 对第 n 次重复中记忆遗忘数量的估计(它应该与
相对应)
- S1 - 一个常数,
使函数 Dev 最小化:
Dev=sqrt(( +
+ ... +
)/RepNo)
=sqr(Laps(1)-
)+sqr(Laps(2)-
)+ ... +sqr(Laps(n)-
))
其中:
- Dev - 描述函数 f 和 g 输出值之间差值的函数,值会在间歇学习期间收集(它反映了数据在实验和理论预测之间的差)
- RepNo - 全部页面上的重复次数总和
- 函数Dev的分项,对应第i页的Dev.
- Laps(j) - 使用函数f和g,分别对第i页和第j次重复计算的遗忘数量,
- 第 i 页、第 j 次重复时的遗忘数量;取自间歇学习期间收集的数据,
- sqrt(x) - x 的平方根,
- sqr(x) - x 的平方。
请注意,只有当函数 f 和 g 简单且定义参数有限时(如 a*ln()+b or a*exp()+b 等),才会有生物学上的思考价值。否则,人们总是可以构建一个巨大的、无意义的公式来自动将 Dev 归零。
解决间歇学习的问题
存档警告:为什么使用文字档案?
这段文字是《优化学习》 作者:Piotr Wozniak (1990) 的一部分
11.2. 间歇学习的解决方案
在搜索使Dev值最小的函数f和g时,我用的是 Wozniak, 1988b 中描述的最小化的数值算法(一种在可行区域内寻找函数局部最大值的新算法。可信论文)。
搜索中使用实例函数如下:
S(1)=x[1]
S(n)=x[2]* *exp(-
*x[3])+x[4])
Laps(n)=x[5]*(1-exp(- /S(n-1)))
其中:
- x[i] - 由最小化程序计算的变量,
- S(n)、Laps(n)、
和
- 如 11.1 中的定义
注意,描述 S(n) 的函数 f 不使用 S(n-1) 作为它的参数(问题的表述允许,但不要求在先前强度的基础上计算新的强度)。
为了保持简易度和节省时间,我设定了在最小化过程中使用 12 个变量的限制。
我测试了大量的数学函数,这些函数是根据有关记忆的明显直觉构建的(例如,随着时间的推移,页面遗忘的数量会增加)。
其中包括指数型、对数型、幂型、双曲线型、S 型、钟型、多项式及一些可能的组合。
在大多数情况下,最小化程序将 Dev 的值减少到 3 以下,函数 f 和 g 的形状类似,与它们的性质独立。
使用少于 12 个变量得到的 Dev 的最小值是 2.887241。
函数 f 和 g 如下:
constant S(1)=0.2104031;
function Sn(Intn,Lapsn,S(n-1));
begin
S(n):=0.4584914*(Intn+1.47)*exp(-0.1549229*Lapsn-0.5854939)+0.35;
if Lapsn=0 then
if S(n-1)>In then
S(n):=S(n-1)*0.724994
else
S(n):=Intn*1.1428571;
end;
function Lapsn(Intn,S(n-1));
var quot;
begin
quot:=(Intn-0.16)/(S(n-1)-0.02)+1.652668;
Lapsn:=-0.0005408*quot*quot+0.2196902*quot+0.311335;
end;在不显著改变Dev的值的情况下,这些函数可以很容易地转换为以下形式:
S(1)=1
for >S(n-1): S(n)=1.5*
*exp(-0.15*
)+1
Laps(n)= /S(n-1)
请注意:
- 只要操作没有明显影响 Dev 的值,函数中的特定元素就会被删除或四舍五入,
- 记忆强度进行了重新缩放,使其可以被解释为一个间隔,其中遗忘数量等于 1,遗忘指数等于 2.5%(一页有 40 个项目,1/40=2.5%),
- 仅当 Intn 不小于 S(n-1) 时,强度公式才有效。这是因为,如果遗忘的数量很低,必须使用 S(n-1) 的值来计算 S(n),例如 Intn <= S(n-1): S(n)=S(n-1)*(1+0.5/1-exp(S(n-1))*(1-exp(-
)))
- 这些公式不能用于描述间隔比最优间隔长很多的过程。这是因为对于
->∞,Laps(n) 的值超过 100%,
- 该公式描述了集体项目的学习,其特点是 E-系数的分布或多或少地均匀。因此,它没能普遍用在难度可变的项目。
就目前而言,上述公式构成了对间歇学习过程的最佳描述,以后将被称为间歇学习模型(简称 IL 模型)
基于间歇学习模型的模拟试验
有了上面发现的公式,我可以进行一系列的模拟实验,帮助我回答许多关于记忆在不同情况下的行为的假设情景。这些模拟实验影响了 SuperMemo 之后多年的进展。特别是,从 SuperMemo 6(1991 )开始,工作量和保留率之间的权衡在优化学习方面起到了重要作用。直到今天,为学习提供指导标准的是遗忘指数(或可提取性),而不是在回忆水平较低时可能出现的、直观自然的记忆稳定性增长。设定记忆遗忘水平起到了下面遗忘指数的作用。
存档警告:为什么使用文字档案?
这段文字选自《优化学习》 ,Piotr Wozniak (1990) 著
11.4. 间歇学习模型的验证
为了验证间歇学习模型与 SuperMemo 理论的一致性,让我们尝试计算出分散重复的最优间隔。
最优间隔由遗忘的数量达到选定值 Lapso 的时刻确定。
算法如下:
1. i:=1
2. S(i):=1
3. 找到 Int(i+1),使 Laps(i+1) 等于 . 使用公式:
Int(n)= *S(n-1) (取自 IL 模型)
其中:
Int(n) 表示第 n-1 个最优间隔。
4. i:=i+1
5. S(i):=1.5*Int(i)*exp(-0.15*)+1(取自 IL 模型)
6. goto 3
如果 Lapso 等于 2.5(遗忘指数 6.25%),而且间歇学习模型参数相同,那么可以观察到惊人的对应关系(比较第 16 页第 3.1 章介绍的实验):
- Rep - 重复的数量
- 间隔 - 重复前的最优间隔,在 IL 模型的基础上由
=2.5 确定,
- 系数 - 最优系数,等于最优间隔除以上一次的最优间隔,
- SM-0 - 在得出 SM-0 算法的实验的基础上计算出的最优间隔
| Rep | 间隔 | 系数 | SM-0 |
|---|---|---|---|
| 2 | 1.8 | 1 | |
| 3 | 7.8 | 4.36 | 7 |
| 4 | 16.8 | 2.15 | 16 |
| 5 | 30.4 | 1.80 | 35 |
| 6 | 50.4 | 1.66 | |
| 7 | 80.2 | 1.59 | |
| 8 | 124 | 1.55 | |
| 9 | 190 | 1.53 | |
| 10 | 288 | 1.52 | |
| 11 | 436 | 1.51 | |
| 12 | 654 | 1.50 | |
| 13 | 981 | 1.50 | |
| 14 | 1462 | 1.49 | |
| 15 | 2179 | 1.49 | |
| 16 | 3247 | 1.49 | |
| 17 | 4838 | 1.49 | |
| 18 | 7209 | 1.49 |
显然,这种确切的对应关系,在某种程度上是一种巧合,因为导致制定 SM-0 算法的实验并不是那么敏感。
值得注意的是,最优系数有逐步降低的趋势!这一事实似乎证实了最近一系列观察,这些观察基于对SM-5 算法 中使用的最优系数矩阵的分析。
如果 Lapso 等于4(遗忘指数 10%,如算法 SM-5),那么最优系数的序列就类似于算法 SM-5中 OF 矩阵的一列。同时,知识保留几乎与 SM-5 数据库中的知识保留理想地匹配。
| Rep | 间隔 | 保留率 | 系数 |
|---|---|---|---|
| 2 | 3 | 93.21678 | |
| 3 | 16 | 93.80946 | 4.89 |
| 4 | 43 | 93.97184 | 2.74 |
| 5 | 102 | 94.04083 | 2.39 |
| 6 | 232 | 94.06886 | 2.27 |
| 7 | 517 | 94.08418 | 2.23 |
| 8 | 1138 | 94.09256 | 2.20 |
| 9 | 2502 | 94.09737 | 2.20 |
| 10 | 5481 | 94.09967 | 2.19 |
保留率是将最优过程中每天的保留率求平均值得到的
R=(R(1)+R(2)+...+R(n))/n
R(d)=100-2.5*Laps(d-dlr)
其中:
- R - 平均保留率
- R(d) - 学习过程中第 d 天的保留率
- Laps(Int) - 间隔 I 天后的期望遗忘数量
- dlr - 最后一次重复的日期
工作量与保留率的权衡
尽管模型使用了异质材料,有些不准确的地方,但对于遗忘指数如何影响学习所需时间,也能可靠地得出结论。这些观察结果经受住了时间的考验:
档案警告:为什么使用文字档案?
这段文字是《优化学习》 作者:Piotr Wozniak (1990) 的一部分
通过比较通过间歇学习模型计算的保留率和工作量数据,可以得出非常有趣的结论:
- 指数 - 遗忘指数(
*2.5)确定了时间最优学习的最优间隔,其中使用 IL 模型安排学习
- 保留率 - 在给定遗忘指数得到的总体保留率(在 10,000 天后计算)
- 重复次数 - 在给定遗忘指数下,在实验过程的前 10,000 天安排的重复次数,
- 系数 - 最优系数的渐近值(取自该过程的第 10000 天)
| 指数 | 保留率 | 重复次数 | 系数 |
|---|---|---|---|
| 2.5 | 97.76 | 两天一次 | 1.0000 |
| 4.5 | 96.88 | 65 | 1.0300 |
| 5.0 | 96.64 | 30 | 1.1600 |
| 5.5 | 96.39 | 22 | 1.3000 |
| 6.25 | 96.01 | 17 | 1.4900 |
| 7.5 | 95.37 | 13 | 1.7700 |
| 10.0 | 94.10 | 10 | 2.1900 |
| 12.5 | 92.78 | 9 | 2.4700 |
图 11.2 表明,用于确定最优间隔的遗忘指数应落在 5-10% 的范围内。
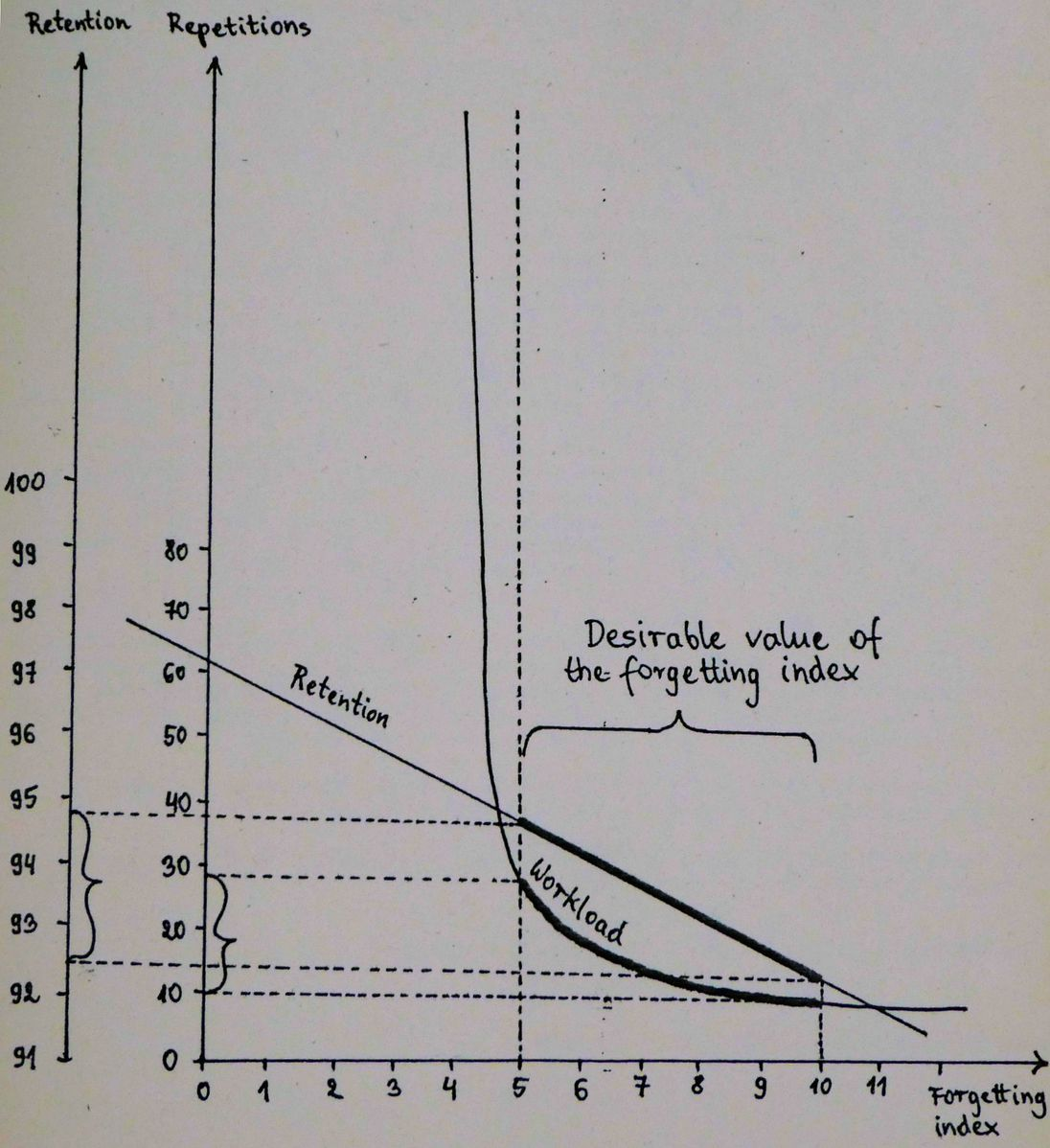
图 11.2 工作量-保留率的权衡:一方面,如果遗忘指数低于 5%,那么工作量就会急剧增加,而不会对保留率产生实质性影响。另一方面,如果遗忘指数超过 10%,工作量几乎没有变化,而保留率却稳步下降。显然,工作量-保留率的权衡直接对应于习得率和保留率之间的妥协。通过增加时间的可用性 X 倍(通过减少工作量 X 倍),可以增加习得率 X 倍(比较第 5 章)。请注意,在这个模型中,遗忘指数和保留率的关系几乎是线性的。(来源:《学习优化》:间歇学习模型,Piotr Wozniak, 1990)
另一重要观察来自使记忆强度增长最大化的遗忘指数的计算过程
由间歇学习模型可得
S(n)=1.5*Laps(n)*S(n-1)*exp(-0.15*Laps(n))+1
对变量 Laps(n) 进行微分后,我们得到:
S'(n)=1.5*S(n-1)*exp(-0.15*Laps(n))*(1-0.15*Laps(n))
最后,令其等于 0,我们得到:
Laps(n)=7.8
这相当于遗忘指数等于 20%!这样的遗忘指数得出的间隔,相当于遗忘指数等于 10% 确定的最优间隔的 2 倍(如SM-5 算法)。然而,别忘了,工作量的唯一权衡因素是知识保留率而不是记忆强度。因此,上述发现并没有令SM-5 算法 失效
结论:间歇学习模型
该章结尾处得出的最终结论经受住了三十年的考验。只有遗忘曲线是非指数形状的说法是不准确的。这是因为这个模型是基于各种性质不同数据建立的,遗忘的指数性质不可显现出来。
档案警告:为什么使用文字档案?
这段文字选自《优化学习》,Piotr Wozniak (1990) 著
临时摘要
- 构建了间歇学习模型,从而能对于不同的重复计划估计其知识保留率
- 该模型确凿地说明,遗忘曲线不是指数型的 [2018 评论:错误的结论:对比遗忘的指数性质]
- 该模型与实验数据吻合良好
- 该模型能以惊人精度求出最优间隔和知识保留率的近似值,而这两个变量是 SuperMemo 模型所隐含的。
- 该模型表明,最优系数在随着重复减少,并渐进接近最终值
- 该模型表明,最节省学习时间的遗忘指数的理想值应落在 5% 至 10% 之间
- 该模型表明,遗忘指数与知识保留率几乎呈线性关系
- 该模型说明,当间隔比 SuperMemo 方法中使用的间隔长约 2 倍时,记忆强度的增幅最大。这相当于遗忘指数等于 20%
下一章:08 1991:启用遗忘曲线

