总目录:0 目录《间隔重复的历史》
上一章:07 1990:记忆的通用公式
Thoughts Memo 汉化组译制
原文:1991: Employing forgetting curves
SuperMemo World 在苦痛中诞生(1991)
1991 年是 SuperMemo 诞生以来最重要的一年。这一年有重大决定,有压力,有大惊小怪、有新发现,更少不了勤勉耕耘。新年伊始,SuperMemo 迎来三个最大的信徒:Biedalak,Murakowski 和我自己。我们都立足于人生旅途上的同一位置:从大学中无忧无虑的岁月走出来,迎面是独立成年生活的不确定性。我们自然而然都梦想着在美国搞高深的科学。Biedalak 梦想研究人工智能,Murakowski 渴望参透量子物理,而我想破解分子层面记忆的秘密。现在回想起来,只要有可喜的成绩单,优秀的标准化考试成绩,以及背景厚实的推荐信,来自东欧国家的研究生在美国是相当受欢迎的。然而如果这些研究生要求全额资助,事情就会变得更加复杂。我身无分文。此外,美国人只把孜孜以求的东方人当成尽职的劳工,对他们自己项目的热情和满腔愿景可能不那么受欢迎。我将永远不会知道。三位信徒对 SuperMemo 都有不同的愿景。
1991 年 1 月 3 日,我开始为 SuperMemo 6 实现新的间隔重复算法。在这同一天,Murakowski 前往伦敦,在那里他将追求他的教育梦想,同时试图销售 SuperMemo 2。他不会通过分销渠道或在商店里销售。他只是挨家挨户地解释程序的优点,好的话能拿到一些钱,不至于丧失信心。
在此期间,我和 Biedalak 定时约着去慢跑 10 公里和冬泳,并在回家的路上一起头脑风暴(我们称之为走谈)。我们主要谈到在美国的学习生涯和如何销售 SuperMemo。在讨论中,开一家我们自己的公司的想法屡屡冒出来,而且愈发频繁。
我开始研发新的间隔重复算法,脑子里有一些想法将永远改变 SuperMemo. SuperMemo 6 中使用的SM-6 算法 是一大突破,这一算法将在之后的 25 年里继续推动软件发展。SM-6 算法将重新采用在 1985 中引导间隔重复发现的简单实验程序,但现在能够自动运行这一实验,收集评分数据,选择最优复习时机:算法将绘制用户的遗忘曲线。这也意味着,用户将能够决定每一个项目可接受的遗忘概率(即保留率-工作量的最优权衡)。
当时,我仍然受限于 360 kB 的软盘(5.25 英寸软盘)。因此,SuperMemo 仍然无法保存所有的重复历史,无法大规模地完全复制 1985 年的方法。然而,在 1990 年 1 月 6 日,我冒出一个简单的想法:我可以只针对不同难度和稳定性类别下的项目收集遗忘曲线数据。我无需维护完整记录,只需要计算即在给定的时间(即在给定的可提取性水平上),在一个给定的类别中,有多少项目留存在记忆中,即可实现类似效果。这个想法作为 SuperMemo 的核心延续至今。即使今天有了重复历史的完整记录,SuperMemo 仍然可以立即知道某个类别中的项目的预期可提取性。
我不断学习,在自由与不确定性交织的氛围中,为 SuperMemo 研究新想法。对我来说,不确定性是能量的源泉。然而,1991 年 2 月 12 日,我得知我母亲确诊为癌症晚期。在自由和不确定性的混合中,这个噩耗平添了一股沉郁气氛。对我来说,沉郁气氛也可以是能量的圆圈。我把学习的时间增加到三倍,全心全意研究癌症,希望能自己找出一些神奇的疗法。看来不合理的乐观主义对生产力有积极影响。它还表明,疯狂的乐观主义可以帮助度过困难时期。通过努力工作,我可以驱散阴霾。高生产力肯定是抗抑郁剂。我的努力工作没有给负面的想法留下空间。我有信心,我会治好我妈妈的病!
顺便说一下,我妈妈确诊的时候,我正在写一个程序来模拟记忆在应对环境时的最优行为。这个程序要从数学上证明记忆的双组分模型是最适合记忆存续的。我一得知妈妈的诊断结果,便把这项工作从我的日程表中扔掉,转去学习癌症知识。我一直没能完成这个程序,这个想法因其他项目而处于不闻不问的境地。
1991 年 3 月 6 日,在我们与 Biedalak 的一次慢跑兼头脑风暴中,有人抛出了 SuperMemo World 这个名字。当时我们无从得知,四个月后,SuperMemo World 将成为我们公司的名字,这家公司至今已成立 27 年。
1991 年 5 月 2 日,我在 SuperMemo 6 中实现了设置目标遗忘指数的选项。1991 年 7 月 5 日,SuperMemo World 诞生了。公司最初的投资之一是一台带有硬盘的个人电脑,我得以摆脱使用软盘时的缓慢速度。
1991 年 11 月 23 日:SuperMemo 被宣布为欧洲软件竞赛的最终胜出者。这个好消息拯救了 SuperMemo World,也是间隔重复的良好开端。
商业化 SuperMemo 的缓慢启动
1991 年 7 月 5 日,当我们与 Krzysztof Biedalak 建立 SuperMemo World 时,未来看起来如此光明,以至于我们需要买墨镜。地球上有很多高智商的人,他们都需要学习。全人类都是我们的市场。唯一的问题是,如何让所有这些聪明人相信,两个在铁幕后受教育的穷学生能为他们提供什么价值。我们不可能用互联网来做这项工作。SuperMemo 比互联网还要古老。由于缺乏资金,我们承担不起广告费用。1991 年的波兰没有风险投资文化。我们能做的就是把最初的几份 SuperMemo 放在文件夹里,然后把它们放在附近的计算机商店的货架上。由于我们的目标是征服全球,我们甚至没做波兰语手册。我们没能做出第一笔买卖。夏天漫长而沉寂,我们心中疑虑悄悄蔓延。

图:1991 年,我们将 DOS 版 SuperMemo 5 的第一批拷贝装在粉红色的文件夹中,贴好贴纸,送到波兹南(波兰)的商店。软件所附的手册没有波兰语翻译。令人惊讶的是,竟有一些买家光顾我们。 1991 年 9 月 9 日至 11 日之间,在 Axe Prim 电脑店,第一笔买卖做成了,可惜该店已不复存在(图片是根据原始文件夹和贴纸重建的)
为什么第一份软件很难卖出去?我可以从我们最早的一个客户的话语中重构这个场景,他真的去了一家商店,看了看公开展示的第一份 SuperMemo。在摆放计算机程序的架子上,与微软公司的闪亮盒子一起,他注意到一个破旧的文件夹,上面写着诱人的文字:「你的突破性快速学习软件」。他拿起文件夹,打开了一本手册,不仅是质量糟糕的复印件,而且是英语。他读到了一个用高高在上的言辞写就的令人难以置信的故事。故事简直是好得天方夜谭:“学习更快”、“知识保留极佳”、“新的科学方法” 以及 “少许耗时” 等等。他没想买下来,整套软件相当昂贵(大约 100 美元,在 1991 年的波兰可是个大数目),然而,他找到了销售人员,想知道 SuperMemo 背后的人是谁。店主对 SuperMemo 相当了解,并解释说。这个故事开始显得很可信。这位顾客一直没有忘记这段插曲。几个月后,他从当地的一些杂志上听说了 SuperMemo,并成为第一批付费客户。他的注册索取券在 1992 年 1 月到达,他的升级历史表明,他用 SuperMemo 用了几十年,现在他的儿子也是常客之一。
然而,在 1991 年夏天,我们一份也没有卖出去。到了秋天,除了我自己之外,每个人都疑虑重重。不是对 SuperMemo,而是对这桩生意的可行性。
知道我们是如何认识的应该会有帮助。与 Biedalak 一起,我是永远的朋友。我和他的兄弟在一个学校上学,我们相距 200 米,并且在波兹南科技大学通过了同一年的计算机科学考试。我不能说我是如何说服 Biedalak 相信 SuperMemo 很不错的。我们只是太亲密了,他一直都在我的朋友圈里。这一部分很容易。Tomek Kuehn 是 SuperMemo 的第一批伟大信徒之一。他也是伟大的程序员,更是伟大的激励者。他一下子就理解了 SuperMemo 的想法。他自己写了两个版本的 SuperMemo:1988 年用于 Atari 800,1989 年用于 Atari ST。1989 年 1 月,他甚至利用一份计算机杂志(Komputer)上的广告卖出了 10 份 SuperMemo 2。我猜想,他没有收回投资的钱,否则他肯定会再次尝试这种伎俩。毕业后,库恩已经有了自己的生意:一家电脑店。这家商店也是最早向客户介绍 SuperMemo 的商店之一。他的伙伴和朋友是 Marczello Georgiew,他也不需要太多的说服力。Georgiew 加入了这个团队。最后,在 1990 年布达佩斯的 GRE 考试中,我遇到了 Janusz Murakowski。他有极佳的数学禀赋,也可能是有史以来最快皈依 SuperMemo 的人。在我们回波兰的火车上,我提到了 SuperMemo。他一下子就被吸引住了。几天后,他已经是 SuperMemo 2 的热心用户(截至 1990 年 6 月 13 日)。在我们公司的说唱歌中,我们唱着「我们是卖 SuperMemo 的人」。要说服人们相信 SuperMemo 能有效果是非常困难的,但团队里的人一直都很热情。
到 1991 年 11 月,人们的热情开始消退。如果我们继续无功而返,我们将逐渐失去与他们的参与和热情成正比的团队。再过几个月,公司可能就要死了。SuperMemo 不会死。我肯定会寻找一个买家,或者以某种方式继续下去。我和这个产品联系得太紧密了。我自己使用它,我所有的知识都投入到我的数据库中。我可能会考虑回到在美国读博士的想法。就像1989年我能够在荷兰的大学里把工作和「下班后」的编程结合起来一样,我可能会继续下去,直到取得一些突破,比如说在网络上。也许这将是一个开放源码的产品?幸运的是,生物聚合物生物化学系的 Wojciech Makalowski 博士建议我们将 SuperMemo 提交给欧洲软件竞赛。由于奇迹般的好运气,我们获得了决赛资格,这立即被波兰媒体,特别是计算机期刊所关注。从那时起,SuperMemo 在波兰媒体中的地位越来越高,越来越吸引人。Andrzej Horodenski 是第一个写关于 SuperMemo 的记者(Computer World 1992)。Pawel Wimmer 是第二个。Wimmer 直到今天仍然是忠实的,他实际上使用了 SuperMemo 2,他可能是在 1989 年在 KOMPUTER 杂志上做广告时从 Tomasz Kuehn 那里得到的。
在成立 1.5 年后,SuperMemo World 终于实现了盈利。还不错。
SuperMemo World 从一开始就是一个奇妙的组合。1991 年,我们在波兰没有风险资本注入资金,所以我们不得不卖起听着像「蛇油」的东西来自力更生。我们如履薄冰,但还是仰仗着激情,信念,以及鸿运当头活了下来。
SM-6 算法的起源
SM-6 算法首次用于 SuperMemo 6(1991),然而,它在 SuperMemo 7(1992)中仍然继续发展。尽管在 Windows 版本中对算法多有修改,但从来没有 SM-7 版本的算法出世。最值得注意的是,从 1994 年起,在 Windows 版 SuperMemo 7 中使用了指数函数来近似遗忘曲线。OF 矩阵的近似也逐步得到了改进。
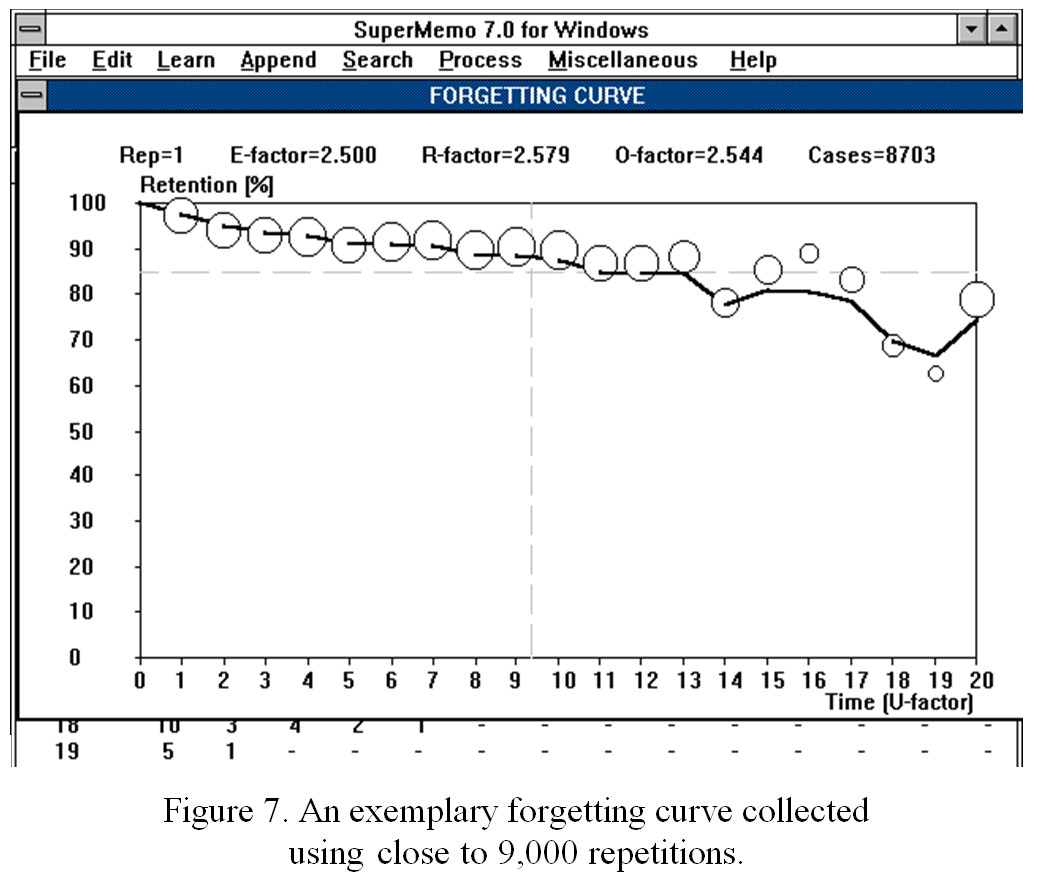
图:Windows 版 SuperMemo 7 是在 1992 年编写的。截至 1992 年 9 月 3 日,它能够显示用户的遗忘曲线图。标有 U-系数的横轴与这个特定图表中的天数相对应。第 14 天和第 20 天之间的奇怪弯曲是很难确定遗忘性质的原因之一。旧的错误假设很难被推翻。直到第 13 天,遗忘似乎几乎是线性的,也可能提供一个良好的指数拟合。我们又花了两年的时间收集数据,最终才找到答案(来源:《SuperMemo 7:用户指南》)
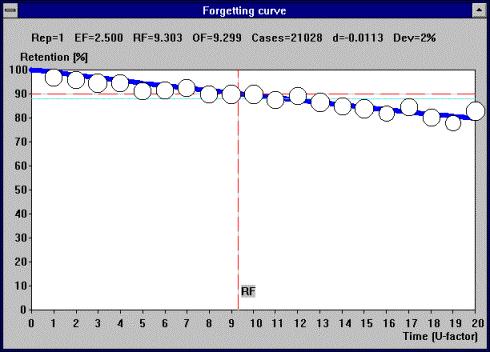
图:用指数函数近似的遗忘曲线,在 Windows 版 SuperMemo 7(1994)上显示。竖轴代表回忆的百分比。横轴用 U-系数 表示时间。该曲线使用 21,000 个重复案例绘制,看起来终于有了规律,足以对遗忘的根本原因作出假设
SM-6 算法有项新功能最为重要,那就是收集遗忘率的数据。有了遗忘曲线,准确地计算最优间隔就很容易了。SM-5 算法中又缓慢又不准确的 bang-bang 方法便告一段落:
存档警告:为什么使用文字档案?
在SM-5 算法 中,确定最优系数矩阵中某项元素的值的过程如下(见上):
- 将初始值设定为以前实验中计算的平均最优系数值(OF)
- 如果目标元素产生的评分(1)大于期望值,则增加 OF,(2)小于期望值则减少 OF,或(3)等于期望值则不改变 OF
上述方法表明,只有经过大量重复,最优系数才能收敛到最优值,最糟糕的是,对于越往后发生的重复,修改—验证的周期(即从改变 OF 矩阵某项的值,到根据这个值计算出下个间隔,由此安排下次重复并由此验证改变的合理性所需的时间)就越长。
介绍遗忘指数的概念
SM-6 算法的新颖之处在于,对最优系数矩阵中给定项对应的遗忘曲线的斜率进行近似,并直接从近似的曲线中计算出新的最优系数的值。换句话说,由于建立了遗忘曲线和最优重复间隔之间的确定性关系,在算法 SM-6 中不需要修改—验证循环。最优系数的修改是在重复后立即发生的,在近似于从包括最近的反馈中提供的评分数据中得出的新遗忘曲线。这种修改不仅使确定最优系数矩阵的最优值的过程大大加快,而且还提供了一种手段来建立在学习过程中将要达到的知识保留的理想水平(见一个示范性的遗忘曲线)。
理想的知识保留水平可由重复中项目里被遗忘的比例得出。这个比例被称为遗忘指数(项目有记住或遗忘之分,依据学生在自我评估其进展时提供的评分 区别)。
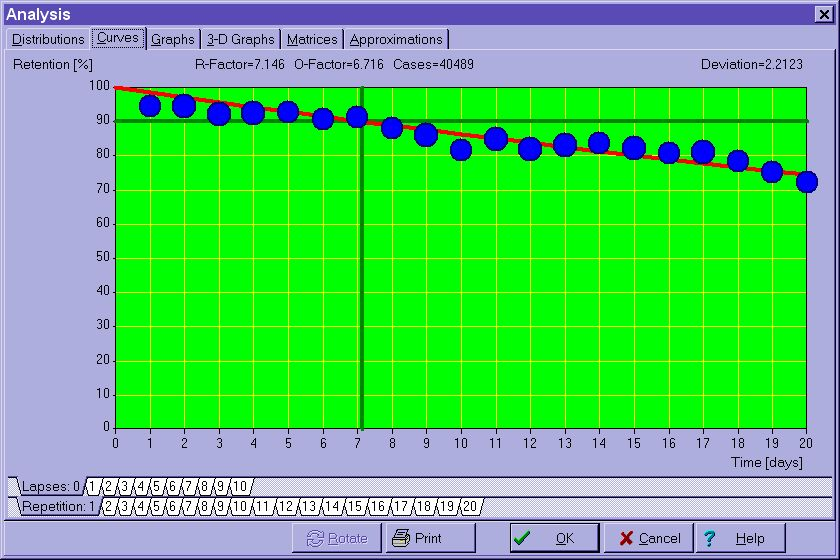
图:由 SuperMemo 8 绘制的重复过程中的示范性遗忘曲线(记录了超过 40,000 个重复案例)。R-系数表明,指数回归指向 7.146 天的最优间隔。然后通过 OF 矩阵将其平滑到 6.176 天。SuperMemo 在这种情况下会为首个间隔取 6 天的值(如果忽略随机散布)
在上图中,时间的推移用间隔来表示,单位是天。纵轴表示以百分比表示的知识保留率。位于 90% 保留率的水平线决定了所要求的遗忘指数,即在重复时项目应该被遗忘的理想比例。然后,最优间隔将自然地出现在所要求的遗忘指数线与遗忘曲线的交叉点上。在上面的例子中,最优间隔等于七天。所提出的遗忘曲线是在 40489 个记录的重复案例的基础上绘制的。关于 R-因子(RF)、O-因子(OF)等数值的解释,请见后面的文字。
直接从遗忘曲线中计算出的最优系数矩阵是高度不规则的,所以在 SM-6 算法中,间隔重复中使用的矩阵,是将保留系数矩阵( RF 矩阵)平滑后的产物,它是直接从与 OF 矩阵 的特定项对应的遗忘曲线得出的。换句话说,遗忘曲线决定了 RF 矩阵中各项元素的取值,但只有将这个矩阵平滑处理,得到 OF 矩阵,才可以用于计算最优间隔
算法 SM-6
下面的算法描述来自我的博士论文,并作了一些澄清,指的是 1994 年的现状:
存档警告:为什么使用文字档案?
- 学到的知识被分割成尽可能小的片段,称为项目
- 项目制定为问题-答案的形式
- 项目是通过自定进度的 drop-out 技术来记忆的,即花时间思考某一问题,直到给出所有正确答案为止
- 从记住一个项目到第一次重复的间隔,对于所有项目都相同。这个间隔是由期望的知识保留水平决定的,这个水平又可以转换为间隔(Wozniak 1994a),只需使用平均遗忘曲线,这一曲线是从普通学生的平均值数据库中提取的。期望的保留率是通过遗忘指数来指定的,这一保留率与重复时遗忘的项目比例相对应(学习如何从遗忘指数计算保留率,反之亦然)。请注意,为了加快优化过程,首次间隔可能会随机缩短或延长(间隔长短不一可以提高遗忘曲线的近似精度)。
- 首个间隔是按照普通学生和普通数据库的预设计算的。然而,一旦遗忘指数的记录值偏离了目标水平,首个间隔的长度就会相应地被修改,其新值来自重复过程中绘制的负指数遗忘曲线的近似。重复评分越多,曲线就会越精确,最优重复间隔的值就会稳定下来,确保目标知识保留率达到指定水平。每次重复后,学生会给出评分,由此可以得知学生是否能准确而轻松地复现正确答案。
- 项目按照评分划分成不同的难度类别。它们的难度在每次连续的重复中被重新估计。每个项目的难度由前面提到的 E-系数(E 代表「容易」(easiness))来描述。对于刚开始学习的所有项目,E-系数都等于 2.5,在随后的重复中会有所修改。例如,评分高于 4, E-系数会增加少许(评分高表明项目容易),而分低于 4 时 E-系数会降低。,以前,E-系数还用来计算,对于某一难度的项目,随着连续重复学习,其间隔长度应该增加多少倍。目前,E-系数只作为最优系数和保留系数矩阵的索引,与实际的间隔增加没有什么关系。
- 项目难度不同,最优间隔也不同
- 项目重复次数不同,间隔也不同
- 为了达到由遗忘指数所决定的期望知识保留率,最优间隔的函数处于不断修正之中。换句话说,该算法将检测学生应对重复的能力,并相应地调整重复间隔的长度。
- 最优间隔的函数表示为最优系数矩阵,简称 OF 矩阵,定义如下:
for n=1: I(n,EF)=OF(n,EF)
for n>1: I(n,EF)=I(n-1,EF)*OF(n,EF)
其中:
- I(n,EF) - 难度 EF 对应的第 n 个间隔
- OF(n,EF) - 第 n 次重复、难度 EF 对应的最优系数
- 最优系数矩阵是通过平滑保留系数矩阵(简称 RF 矩阵)得出的。保留系数矩阵的定义与最优系数矩阵相同。
- 保留系数矩阵的元素被用于估计最优系数矩阵的元素值。每个最优系数对应于一个最优间隔,该间隔在重复时产生所需的保留率(由目标遗忘指数决定)。保留系数矩阵的每个元素都对应于 E-系数和重复次数的不同值
- 保留系数矩阵的元素,称为 R-系数,是由遗忘曲线计算出来的,其形状是根据重复的历史绘制的
- 遗忘曲线图上的时间推移是由 U-系数来衡量的,即当前间隔和前一间隔的比率,不过第一次重复的 U-系数与第一个间隔相等,单位为天(如图)。重复记录使得计算不同 U-系数下的保留率成为可能。保留率与时间推移(U-系数)的关系图代表了一条遗忘曲线。遗忘曲线与所需的保留水平的横截距决定了最优的 R-系数,在对保留系数矩阵进行平滑处理后,可以得到最优的 O-系数
- 每个难度类别和重复次数都有自己的重复记录,用来绘制单独的遗忘曲线。换句话说,项目难度不同,重复次数不同,间隔都有所不同。
- 在学习中使用的间隔取值,包括第一个间隔,都落在最优值的附近,这么做是为了更准确地绘制遗忘曲线,从而提升程序的收敛率。间隔略微分散开来的话,遗忘曲线的近似将使用图形上更分散的点集
下一章:09 1994:遗忘的指数性质

